लसावि (LCM) : लघुत्तम सामाईक विभाज्य Least Common Multiple
ल.सा.वि. : LCM- Least Common Multiplie : लघुत्तम सामाईक विभाज्य म्हणजे अशी लहानात लहान संख्या जिला दिलेल्या सर्व संख्यांनी भाग जातो. म्हणजे यासंख्येपेक्षा सर्व संख्यांनी भाग जाणारी लहान संख्या नसते.
मसावि (HCF) : महत्तम सामाईक विभाज्य Highest Common Multiple
म.सा.वि. : HCF – Highest Common Factor : महत्तम सामाईक विभाजक म्हणजे अशी मोठ्यात मोठी संख्या जिने दिलेल्या सर्व संख्यांना भाग जातो. म्हणजे यासंख्येपेक्षा सर्वांना भाग जाणारी मोठी संख्या नसते.
विभाज्य (Multiple) :
1, 2, 3, 4, 6, 12 ह्या संख्यांनी 12 ला पूर्ण भाग जातो. म्हणुन 12 हि संख्या 1, 2, 3, 4, 6, 12 ची विभाज्य संख्या आहे.
विभाजक (Factors) :
12 ला 1, 2, 3, 4, 6, 12 ने पूर्ण भाग जातो म्हणुन ह्या संख्या 12 च्या विभाजक आहेत.
मसावि (HCF) :
12 व 16 ला 4 ह्या मोठ्यात मोठ्या संख्येने पूर्ण भाग जातो. 4 हि संख्या 12 व 16 चा मसावि आहे.
लसावि (LCM) :
2, 4 व 6 ह्या संख्यांनी 12 ह्या लहानात लहान संख्येला पूर्ण भाग जातो. म्हणुन 12 हि संख्या 2, 4 व 6 चा लसावि आहे.
- जोडमुळ (Twin – Prime) संख्यांचा मसावि 1 असतो,
- सहमुळ (Co-Prime) संख्यांचा मसावि 1 असतो.
- जोडमुळ (Twin – prime) संख्यांचा लसावि त्यांचा गुणाकार असतो.
- सहमुळ (Co-Prime) संख्यांचा लसावि त्यांचा गुणाकार असतो.
- दोन क्रमागत सम संख्यांचा मसावि 2 असतो.
- दोन क्रमागत सम संख्यांचा लसावि हा त्यांच्या गुणाकाराच्या अर्धा असतो.
- दोन कमान विषम संख्यांचा मसावि 1 असतो.
मसावि काढण्याच्या पद्धती :
१) विभाजक पद्धती २) भागाकार पद्धत
३) मुळ अवयव पद्धत ४) अंकगणिताचा मुलभुत सिद्धांत
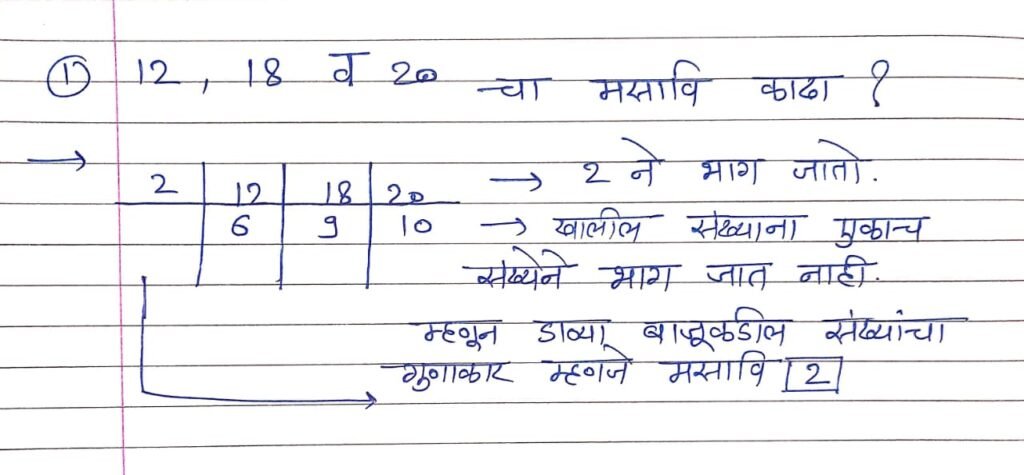
- Step 1 : दिलेल्या सर्व संख्या आडव्या मांडून घ्याव्या. त्यांचे बॉक्स तयार करा.
- Step 2 : आता दिलेल्या सर्व संख्यांना एकाच संख्येने भाग दयावा. त्यानंतर पुन्हा उरलेल्या सर्व संख्यांना एकाच संख्येने भाग जात असेल तर दयावा व सर्व संख्यांना एकाच संख्येने भाग जात नसेल तर डाव्या बाजुकडील संख्यांचा गुणाकार म्हणजे मसावि होय.
- थोडक्यात मसावि अट : सर्व संख्यांना एकाच संखेने भाग जावा.
Base Level Questions :
लसावि काढण्याच्या पद्धती :
१) मुळ अवयव पद्धत २) विभाज्य पद्धत
३) अंकगणिताचा मुलभुत सिद्धांत
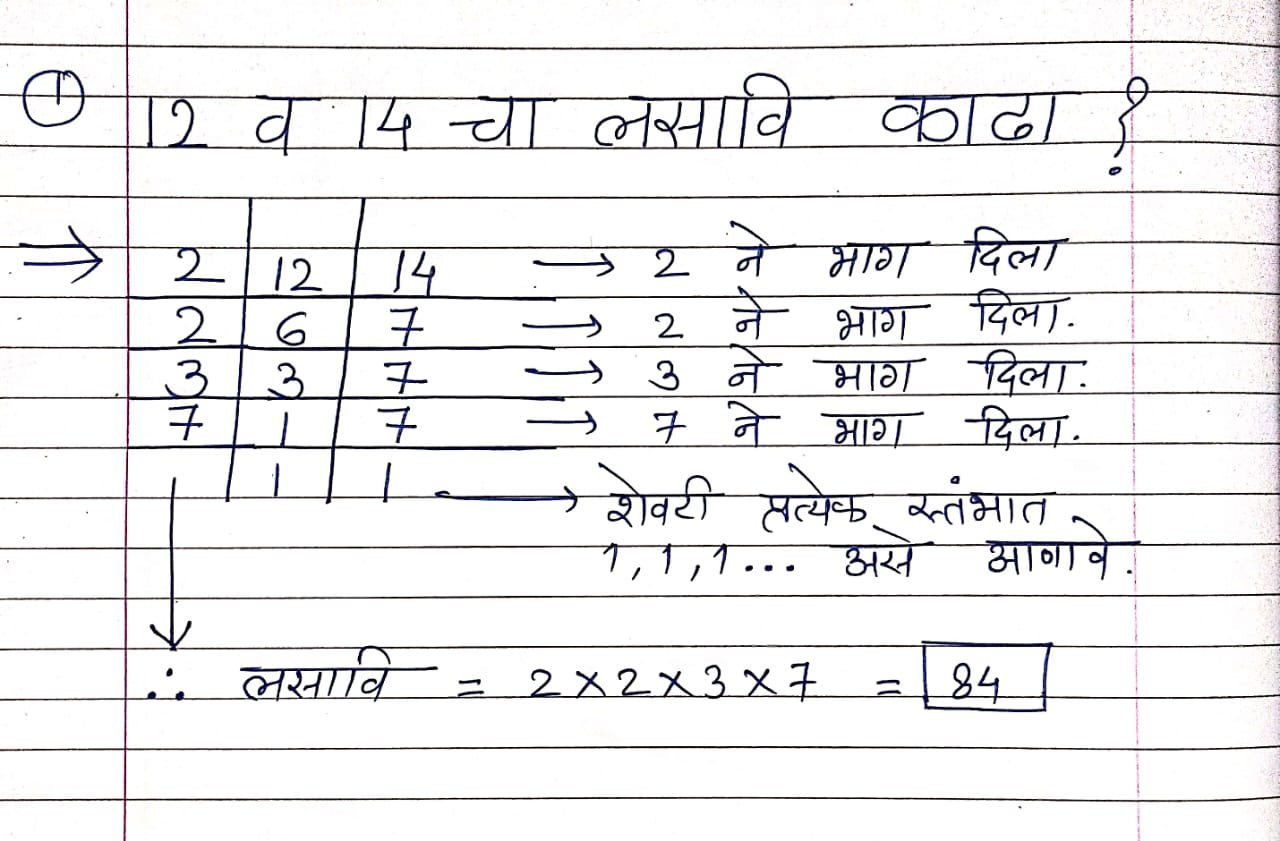
- Step 1 : दिलेल्या सर्व संख्या आडव्या मांडून घ्याव्या. त्यांचे बॉक्स तयार करा.
- Step 2 : आता दिलेल्या सर्व संख्यांना एकाच संख्येने भाग दयावा. त्यानंतर पुन्हा उरलेल्या सर्व संख्यांना एकाच संख्येने भाग जात असेल तर दयावा व सर्व संख्यांना एकाच संख्येने भाग जात नसेल तर डाव्या बाजुकडील संख्यांचा गुणाकार म्हणजे मसावि होय.
- Step 3 : त्यानंतर लसावि काढण्यासाठी उरलेल्या कमीत कमी
- दोन संख्यांना जरी एकाच संख्येने भाग गेला, तरी दयावा. जोपर्यंत कमीत कमी दोन संख्यांना एकाच संख्येने भाग जातो तो पर्यंत दयावा व नंतर डाव्या बाजूकडील सर्व संख्यांचा गुणाकार गुणिले उरलेल्या संख्या यांचा गुणाकार म्हणजे लसावि होय.
- थोडक्यात लसावि अट : कमीत कमी दोन संख्यांना एकाच संखेने भाग जावा.
Base Level Questions :
२) 7 व 13 चा लसावि काढा ?
= मूळ संख्यांचा लसावि त्यांच्या गुणाकारा इतकाच असतो .
= 7 व 13 चा लसावि = 13 × 7 = 91
३) 2, 4, 8, 16, 64 चा लसावि काढा?
= दिलेल्या गटातील सर्वात मोठ्या संख्येला जर उर्वरित सर्व संख्यांनी भाग जात असेल, तर ती मोठी संख्या त्या गटाचा लसावि असते.
वरील गणितात 64 ला 2, 4, 8, 16 ने पूर्ण भाग जातो म्हणून लसावि 64 घ्यावा.
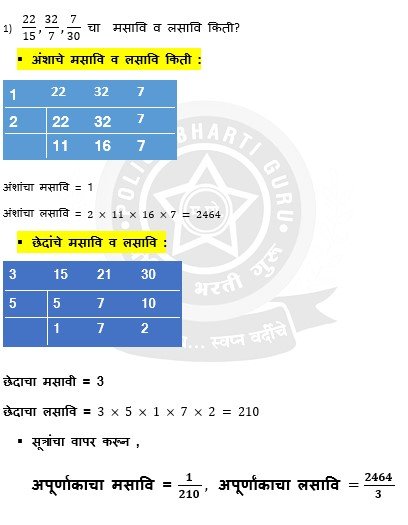
अपूर्णांकाच्या मसावि व लसावि काढणे : –

दशांशाचा मसावि व लसावि काढण्याची पद्धत :
प्रश्न. 1) 22.5, 0.75 व 15 चा मसावि व लसावि काढा.
उत्तर : Step 1 : सर्व संख्यामध्ये दशांशानंतरचे अंक सारखे करून घ्यावे. 22.5 मध्ये दशांशानंतर 1 अंक आहे. 0.75 मध्ये दशांशानंतर 2 अंक आहेत. व 15 मध्ये दशांशानंतर एकही अंक नाही. 22.50, 0.75, 15.00 याप्रमाणे सर्व संख्यांत आता दशांशानंतर दोन अंक करून घेतले.
Step 2 : आता दशांश नाही असे गृहित धरून नेहमीच्या पद्धतीने मसावि व लसावि काढावा.
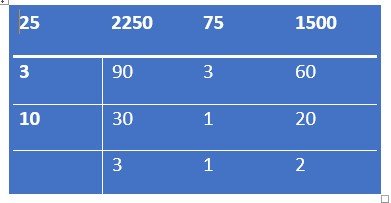
मसावि = 75,
लसावि = 25 × 3×10×3×1 × 2 = 4500
Step 3 : आता आपण step 1 मध्ये सर्व संख्यांमध्ये दशांशानंतर 2 अंक करून घेतले असल्याने या आलेल्या मसावि व लसाविच्या डावीकडे 2 अंक दशांश दयावा.
(उत्तर : मसावि = 0.75 लसावि = 45.00)
मसावि व लसावि वरील इतर प्रकारची उदाहरणे :
सूत्र : 1 ली संख्या × 2 री संख्या = मसावि × लसावि
1) दोन संख्यांचा गुणाकार 2160 आहे. मसावि 12 असल्यास लसावि किती?
उत्तर : दोन संख्यांचा गुणाकार = मसावि × लसावि
2160 = 12 × लसावि

सूत्र : = असमाईक अवयवांचा गुणाकार
मोठी संख्या = मोठा असामाईक अवयव × मसावि
लहान संख्या = लहान असामाईक अवयव × मसावि
1) लसावि 510 व मसावि 34 असल्यास लहान संख्या सांगा?
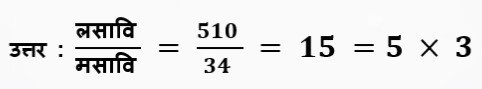
मोठी संख्या = मोठा असामाईक अवयव × मसावि = 5 × 34 = 170
लहान संख्या = लहान असामाईक अवयव × मसावि = 3 × 34 = 102